Last Update: Nov. 29, 2025
Key goals of this assignment are to (1) practice using arrays, in particular, 2 dimensional arrays; (2) design loops with complex loop structure; and (3) practice reading data from an input file.
Due: 11:55 PM, Sunday Dec. 7, 2025
IMPORTANT: The best advice we can give you about PS8 is to carefully test, debug, and re-test your code as you write it. Do not attempt to write a whole program at once—if you do, then you may have no idea where to find the error if the program doesn't work. Proactive testing will save you enormous amounts of time in the long run. Trust us!
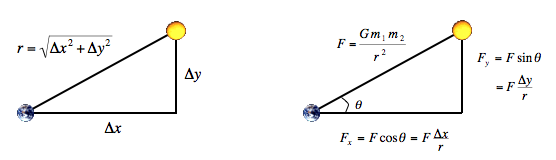
The physics. We review the equations governing the motion of the particles, according to Newton's laws of motion and gravitation. Don't worry if your physics is a bit rusty; all of the necessary formulas are included below. We'll assume for now that the position (rx, ry) and velocity (vx, vy) of each particle is known. In order to model the dynamics of the system, we must know the net force exerted on each particle.

The numerics. We use the leapfrog finite difference approximation scheme to numerically integrate the above equations: this is the basis for most astrophysical simulations of gravitational systems. In the leapfrog scheme, we discretize time, and update the time variable t in increments of the time quantum Δt (measured in seconds). We maintain the position (rx, ry) and velocity (vx, vy) of each particle at each time step. The steps below illustrate how to evolve the positions and velocities of the particles.
Your program will create an animation to illustrate the preceding. We have practiced animation in PS4 and hence this should not be hard. Specifically, your program draws each particle at its current position using standard drawing, and repeats this process at each time step until a designated stopping time. By displaying this sequence of snapshots (or frames) in rapid succession, you will create the illusion of movement. After each time step (i) draw the background image starfield.jpg, (ii) redraw all the bodies in their new positions, and (iii) control the animation speed using StdDraw.show().
Executing your program. We ask that you name your program NBody.java. To practice program control from the commandline (i.e., Command Prompt or Terminal), we ask that you give NBody input parameters from the commandline, where the first two arguements have type double and specify T and Δt. The third argument specifies the file name (assume no space in the file name) specifying the universe (see below). An example is:
% java NBody 157788000.0 25000.0 planets.txt
After reading the command line, your program:
Universe file: The input file to specifiy a universe is a text file that contains the information for a particular universe. The first value is an integer N which represents the number of particles. The second value is a real number R which represents the radius of the universe: assume all particles will have x- and y-coordinates that remain between -R and R. Finally, there are N rows, and each row contains 6 values. The first two values are the x- and y-coordinates of the initial position; the next pair of values are the x- and y-components of the initial velocity; the fifth value is the mass; the last value is a String that is the name of an image file used to display the particle.
As an example, planets.txt contains data for our solar system (in SI units).
5 2.50e+11 1.4960e+11 0.0000e+00 0.0000e+00 2.9800e+04 5.9740e+24 earth.gif 2.2790e+11 0.0000e+00 0.0000e+00 2.4100e+04 6.4190e+23 mars.gif 5.7900e+10 0.0000e+00 0.0000e+00 4.7900e+04 3.3020e+23 mercury.gif 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 1.9890e+30 sun.gif 1.0820e+11 0.0000e+00 0.0000e+00 3.5000e+04 4.8690e+24 venus.gif
When reading a universe file, NBody should read in exactly as many rows of body information as are indicated by N, the first value in the file. Maintain several parallel arrays to store the data. To make the computer simulation, write a loop that repeatedly updates the position and velocity of the particles. Before plotting, use StdDraw.setXscale(-R, +R) and StdDraw.setYscale(-R, +R) to scale the physics coordinates to the screen coordinates.
Your browser can not display this movie.
Be sure that Javascript is enabled and that you have Flash 9.0.124 or better.
We provide a set of examples and data at
A brief description of the files:Print the information back out in the specified format. Our input files were created with the following System.out.printf() statements.
System.out.printf("%d\n", N);
System.out.printf("%.2e\n", R);
for (int i = 0; i < N; i++) {
System.out.printf("%11.4e %11.4e %11.4e %11.4e %11.4e %12s\n",
rx[i], ry[i], vx[i], vy[i], mass[i], image[i]);
}
Right now, you are printing the information to aid in debugging;
later, you will use this code to print out the state of the universe
at the end of the simulation.
Do not even think of continuing until you have tested and debugged this part.

Here are our results for a few sample inputs.
% java NBody 0.0 25000.0 planets.txt // zero steps 5 2.50e+11 1.4960e+11 0.0000e+00 0.0000e+00 2.9800e+04 5.9740e+24 earth.gif 2.2790e+11 0.0000e+00 0.0000e+00 2.4100e+04 6.4190e+23 mars.gif 5.7900e+10 0.0000e+00 0.0000e+00 4.7900e+04 3.3020e+23 mercury.gif 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 1.9890e+30 sun.gif 1.0820e+11 0.0000e+00 0.0000e+00 3.5000e+04 4.8690e+24 venus.gif % java NBody 25000.0 25000.0 planets.txt // one step 5 2.50e+11 1.4960e+11 7.4500e+08 -1.4820e+02 2.9800e+04 5.9740e+24 earth.gif 2.2790e+11 6.0250e+08 -6.3860e+01 2.4100e+04 6.4190e+23 mars.gif 5.7875e+10 1.1975e+09 -9.8933e+02 4.7900e+04 3.3020e+23 mercury.gif 3.3087e+01 0.0000e+00 1.3235e-03 0.0000e+00 1.9890e+30 sun.gif 1.0819e+11 8.7500e+08 -2.8329e+02 3.5000e+04 4.8690e+24 venus.gif % java NBody 50000.0 25000.0 planets.txt // two steps 5 2.50e+11 1.4959e+11 1.4900e+09 -2.9640e+02 2.9799e+04 5.9740e+24 earth.gif 2.2790e+11 1.2050e+09 -1.2772e+02 2.4100e+04 6.4190e+23 mars.gif 5.7826e+10 2.3945e+09 -1.9789e+03 4.7880e+04 3.3020e+23 mercury.gif 9.9262e+01 2.8198e-01 2.6470e-03 1.1279e-05 1.9890e+30 sun.gif 1.0818e+11 1.7499e+09 -5.6660e+02 3.4998e+04 4.8690e+24 venus.gif % java NBody 60000.0 25000.0 planets.txt // three steps 5 2.50e+11 1.4958e+11 2.2349e+09 -4.4460e+02 2.9798e+04 5.9740e+24 earth.gif 2.2789e+11 1.8075e+09 -1.9158e+02 2.4099e+04 6.4190e+23 mars.gif 5.7752e+10 3.5905e+09 -2.9682e+03 4.7839e+04 3.3020e+23 mercury.gif 1.9852e+02 1.1280e+00 3.9705e-03 3.3841e-05 1.9890e+30 sun.gif 1.0816e+11 2.6248e+09 -8.4989e+02 3.4993e+04 4.8690e+24 venus.gif % java NBody 31557600.0 25000.0 planets.txt // one year 5 2.50e+11 1.4959e+11 -1.6531e+09 3.2949e+02 2.9798e+04 5.9740e+24 earth.gif -2.2153e+11 -4.9263e+10 5.1805e+03 -2.3640e+04 6.4190e+23 mars.gif 3.4771e+10 4.5752e+10 -3.8269e+04 2.9415e+04 3.3020e+23 mercury.gif 5.9426e+05 6.2357e+06 -5.8569e-02 1.6285e-01 1.9890e+30 sun.gif -7.3731e+10 -7.9391e+10 2.5433e+04 -2.3973e+04 4.8690e+24 venus.gif
Can I combine Steps 1, 2, and 3 into one massive loop? No! You must do Step 1 (compute all of the forces) before Steps 2 and 3 (moving and drawing them); otherwise, you will be computing the forces at time t using the positions of some of bodies at time t and others at time t + Δt. Of course, the three steps comprise the body of the main simulation loop.
I draw the bodies, but nothing appears on the screen. Why? Use StdDraw.setXscale() and StdDraw.setYscale() to change the coordinate system to use the physics coordinates instead of the unit box.
My bodies repel each other. Why don't they attract each other? Make sure that you get the sign right when you apply Newton's law of gravitation: (x[j] - x[i]) vs. (x[i] - x[j]). Note that Δx and Δy can be positive or negative so do not use Math.abs(). Do not consider changing the universal gravitational constant G to patch your code!
How should I compute x2? The simplest way is x*x. In Java, the ^ operator means XOR (not exponentiation). Don't use Math.pow(x, 2).
What is Δx? It's the change in x-coordinate between two bodies (not between a body at time t and at time t + Δt).
How many steps should my program simulate if T is not a multiple of ΔT? Simulate the universe as long as t < T. For example, if T is 50,000 and ΔT is 25,000, you should simulate the system for two steps (t = 0 and 25,000). If T is 60,000 and ΔT is 25,000, you should simulate the system for three steps (t = 0, 25,000 and 50,000).
Does my program need to plot anything if T equals 0? No, you do not need to plot anything.
Everything works until I add StdAudio.play("2001.mid") then everything hangs. What do I do? On some machines there may be a race problem between sending things to the drawing window and sending things to the sound card. Try moving StdAudio.play() to a place in the program after your initial calls to StdDraw.setXscale() and StdDraw.setYscale(). If it still does not work, please use 2001theme.wav.
I can play MP3s using my favorite media player, but no sound plays in Java. What could be wrong? If you are running Windows, be sure that the audio stream that Java uses is not muted via Start -> Programs -> Accessories -> Multimedia -> Volume Control -> Wave Out.
Here's a more complete explanation of how you should interpret the variables. The classic Euler method updates the position uses the velocity at time t instead of using the updated velocity at time t + Δt. A better idea is to use the velocity at the midpoint t + Δt / 2. The leapfrog method does this in a clever way. It maintains the position and velocity one-half time step out of phase: At the beginning of an iteration, (rx, ry) represents the position at time t and (vx, vy) represents the velocity at time t - Δt / 2. Interpreting the position and velocity in this way, the updated position (rx + Δt vx, ry + Δt vy). uses the velocity at time t + Δt / 2. Almost magically, the only special care needed to deal with the half time-steps is to initialize the system's velocity at time t = -Δt / 2 (instead of t = 0.0), and you can assume that we have already done this for you. Note also that the acceleration is computed at time t so that when we update the velocity, we are using the acceleration at the midpoint of the interval under consideration.
This part of the assignment explores array, nested loop, and indefinite loop control in the context of solving a common puzzle. In particular, we have finally learned enough about Java to be able to write a program that will solve many different types of Sudokus. Note that the program as we specified will not solve any possible Sudoku that could possibly exist, although you could probably write such a program on your own if you want.
Step 1: Check A Specific Position:
Write a method with the following signature:
public static boolean isPossible(int[][] sudoku, int row, int column, int numToCheck)
that, given a Sudoku (represented as a two-dimensional array), a
row number, a column number, and a number to check to see if it could
possibly go in the square in the Sudoku at the given row and column
(counting from 0). The method will return false if we can be sure that
this number cannot go in that square (because that same number already
exists in the same row, column, or 3 by 3 box; the method returns true
otherwise. For example, let's say we have the following Sudoku:
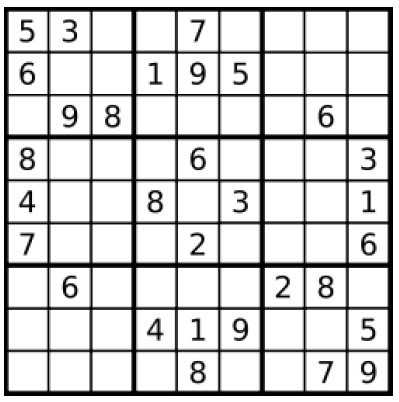
Assume that this Sudoku is read into a two dimensional array called sudoku in the main method. If we call:
isPossible(sudoku, 8, 5, 7)the method should return 'false' because there is a 7 in the same row (remember that we are counting from 0, so when we called the method with the values of '8' and '5' for the row and column parameters, we are really asking about the 9th (last) row and 6th column in that row, and there is already a 7 in the last row of the sudoku). Similarly, if we call:
isPossible(sudoku, 8, 5, 3)the method should return 'false' because there is a 3 in the same column (the 6th column of the Sudoku). Similarly, if we call:
isPossible(sudoku, 8, 5, 4)the method should return 'false' because although there is not a 4 in the same column or in the same row, there is a 4 in the same 3 x 3 box (for those students who are not familiar with sudokus: a sudoku is divided into nine different 3 x 3 boxes, corresponding to the darker black lines in the image above).
However, if we call:
isPossible(sudoku, 8, 5, 2)the method should return 'true' because there is currently no 2 in the same row, column, or 3 x 3 box of sudoku[8][5]. (In fact, if we were to solve the entire Sudoku, we would find out that the correct number to place in this box is '6', not '2'; however, at this point, we are unable to rule out '2' as a possibility for this box, so the method should return true.)
Step 2: Enumerations
Now that we have the isPossible method working, let's use it to solve sudokus! Associated with this problem set are 8 sample sudokus. Your task in this part of the assignment is to write a program that solves all of them except samplesudoku4.txt, using the following algorithm.
We know that each row, column, and 3x3 box in a Sudoku must include each number '1' through '9'.
For example, in the Sudoku pictured above (which, by the way, is the same as samplesudoku8.txt that is provided by this assignment), when we check the bottom-right 3x3 box for the number '1' (which is part of step 3 in the above algorithm), there are 4 empty squares we could check. isPossible returns false for the top-right square in this 3x3 box, because there is a '1' in the same column. It returns false for both of the empty squares in the second row of the 3x3 box because there is a '1' in the same row. However it returns true for the bottom-left square of the 3x3 box. Since it returned true only once for the whole 3x3 box, we know that we can solve the bottom-left square of the bottom-right 3x3 box with the number '1'.
Keep on running steps 1 through 3 of the above algorithm until none of them are able to solve any more squares. At that point, either the entire Sudoku has been solved, or we simply have to give up (as we have to do for samplesudoku4.txt). A suggested control structure implementing the preceding is:
boolean hasMadeProgress; do hasMadeProgress = false; apply the rules; if figure out a new entry, hasMadeProgress = true; while (hasMadeProgress);
You should start with the SudokuSolver.java file that is provided by this assignment. The first few lines of the main method of the assignment are hard-coded to read a file name (e.g., samplesudoku8.txt) from the command line, set up a Scanner that you can use to read the file, and also declare a multi-dimensional array called 'sudoku'. When you test your program, you can specify through the command line any of the 8 sample sudoku files that we provide you. When developing your program, you may want to hardcode a particular sudoku input without the need of input from commandline. But when you submit the assignment, please keep the lines marked do not change as indicated in SodukuSolver.java.
'Steps' here represent the three steps in the algorithm in 'Step 2: Enumerations'.
If you repeatedly apply step 1 of the above algorithm, you will be able to solve samplesudoku8.txt in addition to samplesudoku1.txt, samplesudoku2.txt, and samplesudoku3.txt. So we suggest that you get step 1 working first and make sure that this solves these four sample sudokus. Once you are sure that step 1 is working correctly, start working on incorporating step 2. If you get step 2 working and repeatedly apply both step 1 and step 2, you will also get samplesudoku5.txt and samplesudoku7.txt solved. However, you will need to get step 3 working in order to solve samplesudoku6.txt. You can find all of the files from this link:
Please make sure you submit all required files. Remember that you always need to include the header for your .java files. For Part 1, please submit NBody.java and other files if you need. For Part 2, please submit SudokuSolver.java and any other files if you need.
//******************************************************************* // // File: FileName.java Assignment No.: 8 // // Author: <your name> Email: <your email> // // Class: ClassName // // Time spent on this problem: // -------------------- // Please give a description about your design. // // // Report file name: //*******************************************************************
The submission repository for ps8 is https://gitee.com/simmonsong/ct-xmuf25-ps8.
Please follow the instructions in Assignments Submission to submit your assignments.
Git introduction is a help document for git utilization..
Enjoy!